LC141,142

本次主题是leetcode141、142环形链表的解法；

在阅读前，你需要了解：链表/环形链表基础知识，基础mod运算,
LC141 环形链表 I、LC142 环形链表 II的题目。
LC141 环形链表 I:

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。 否则，返回 false 。

LC142 环形链表 II:

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

·说明：不允许修改给定的链表。
·进阶：
你是否可以使用 O(1) 空间解决此题？

对于LC141:

我们采用快慢指针的解法，设快指针为P_fast，慢指针P_slow，快指针每次向前走两个节点，慢指针每次走一个节点，若二者最终相遇，即快指针在环内追上了慢指针，则我们可以认为该链表存在环。（这就好比两个人在操场跑步，跑的快的人一定会与慢的相遇）；如果这个不能理解的话建议/remake；

对于LC142:

很明显这题要求更高了，不仅需要判断是否有环，还需要我们需要返回环的起始节点；
看到这题第一眼，我直接想到的是利用哈希表（HashSet），利用哈希表未免有点捞，我就不写了；当然，如果你不懂哈希表，而且追求更小的空间复杂度(O(1))，请继续往下看；

模仿LC141，我尝试再次使用快慢指针的方式来解，尝试分析一下当快慢指针相遇时的具体情况：
首先设定一个链表，假设其含有头节点，如下：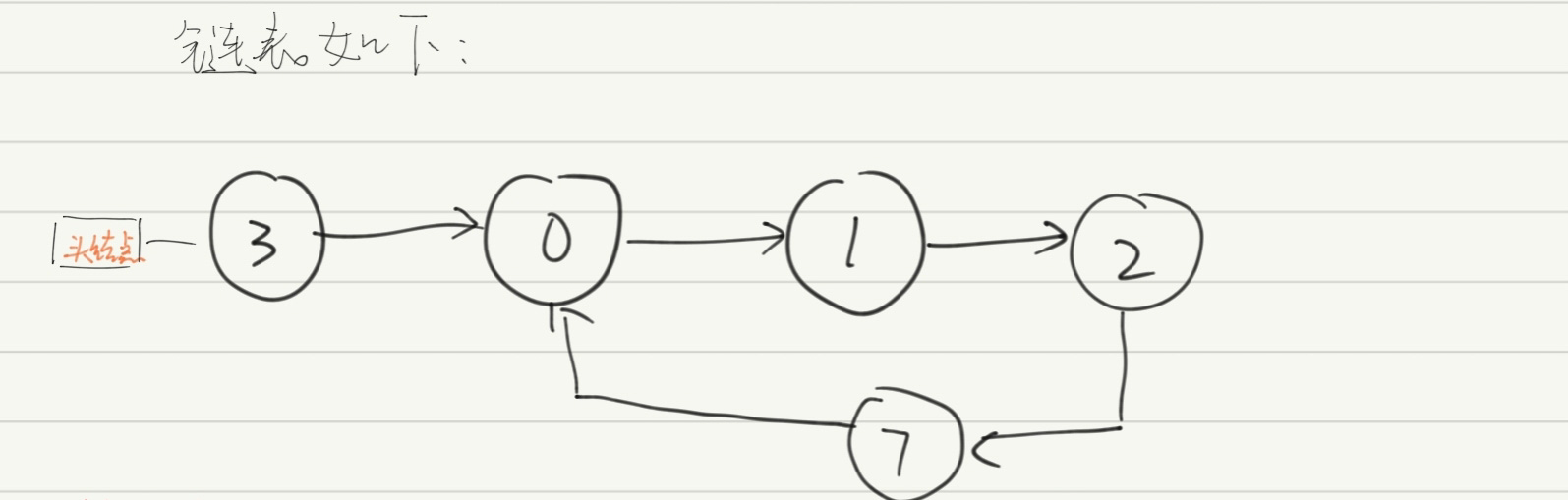

经分析可得两个结论

第一个结论
仍旧设快指针为P_fast，慢指针P_slow，快指针每次向前走两个节点，慢指针每次走一个节点；
为了方便理解，上一句话可以等同于：P_fast速度为2节点/次,P_slow速度为1节点/次；
我们假设快慢指针都走了k次，最后有：快指针总路程=2k，慢指针总路程=k；
若二者在环中相遇，可得(2k-num₁) mod num_环 =(k-num₁) mod num_环;
直观理解如下：

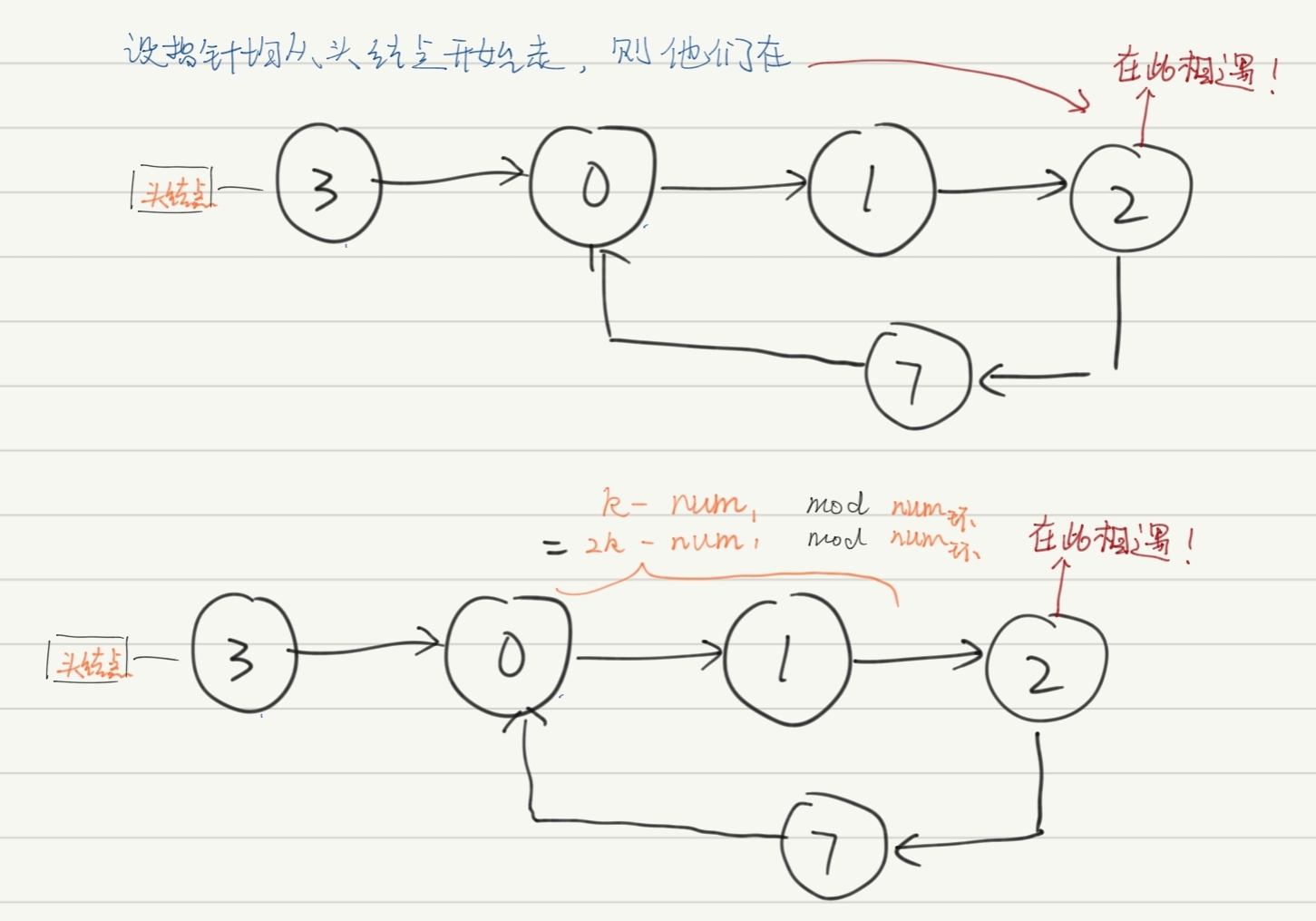
注意，此处num_环=环包含的节点数，num₁=总节点数-num_环;
直观理解如下：

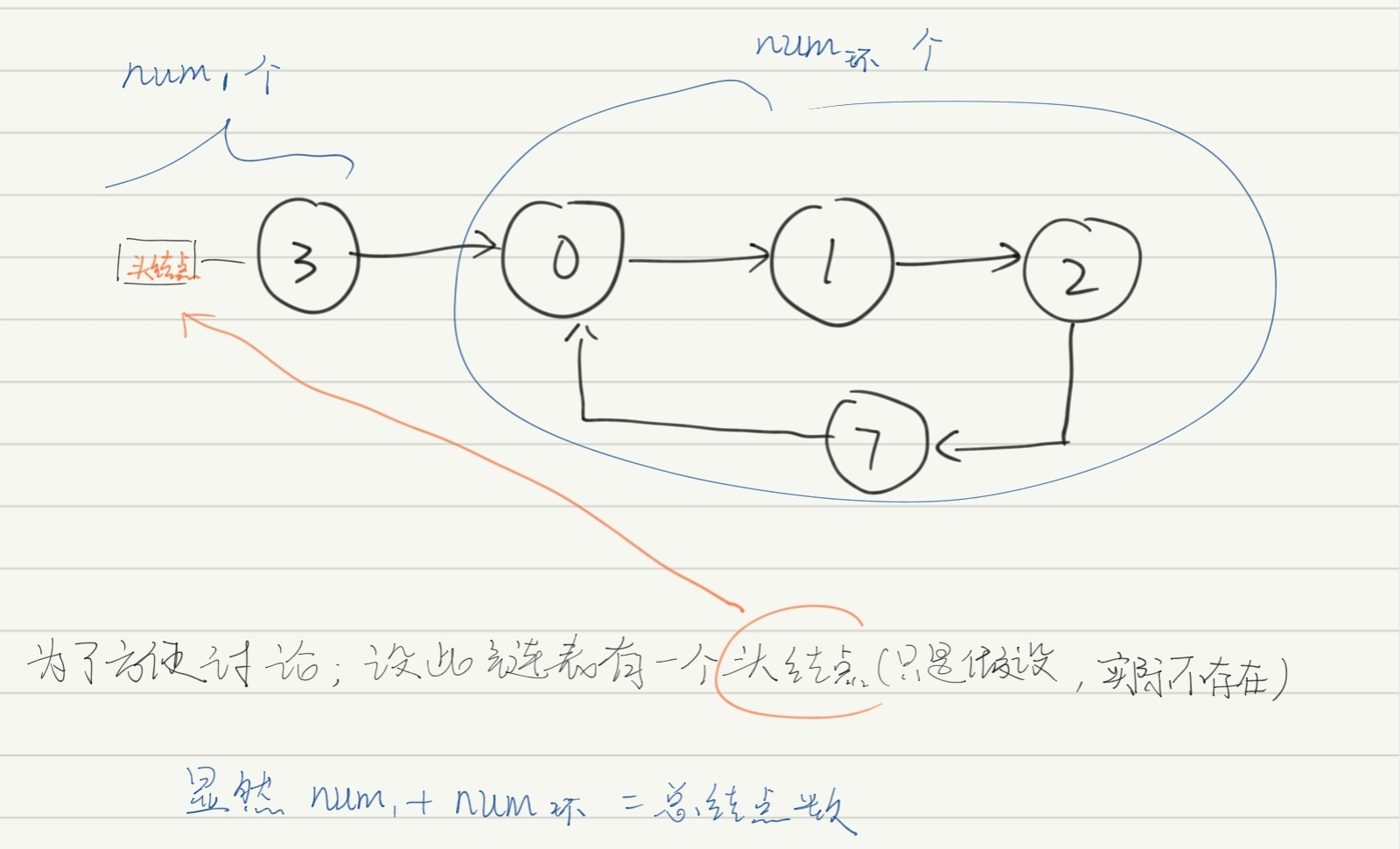
接下来我们对(2k-num₁) mod num_环 =(k-num₁) mod num_环进行化简:

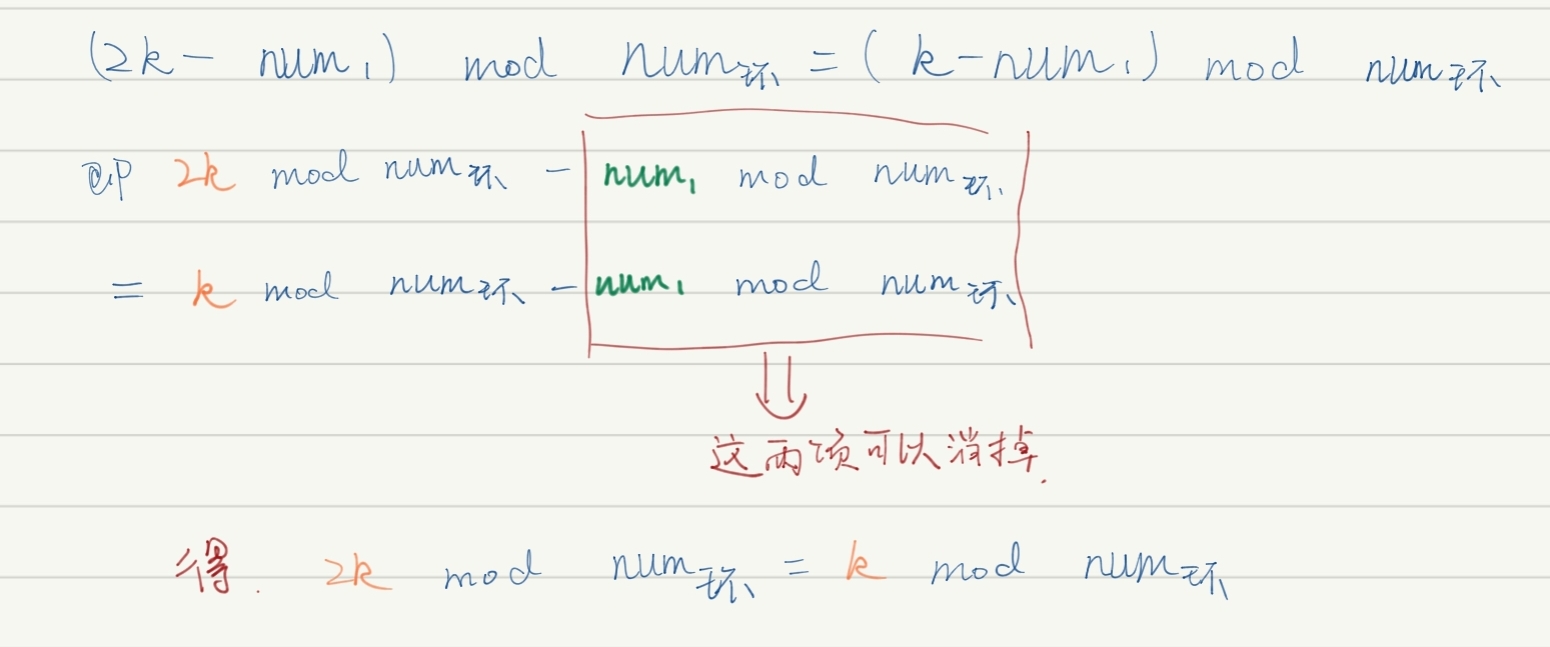
目前为止，我们化简得到了2k mod num_环=k mod num_环；
请各位想象一下：在什么情况下，2k和k除以num_环(k、num_环均为任意正整数)，余数相同？
显然是余数为0的时候(这里不做过多赘述，本文末有详细证明).
至此我们得出了第一个结论①：k为num_环整数倍，我简记作k=a·num_环（a为任意正整数);
我们继续在此结论基础上分析：已知k=a·num_环，能否尝试分析出此处a的值？答案是可以，请继续看第二个结论。
第二个结论
Step1：

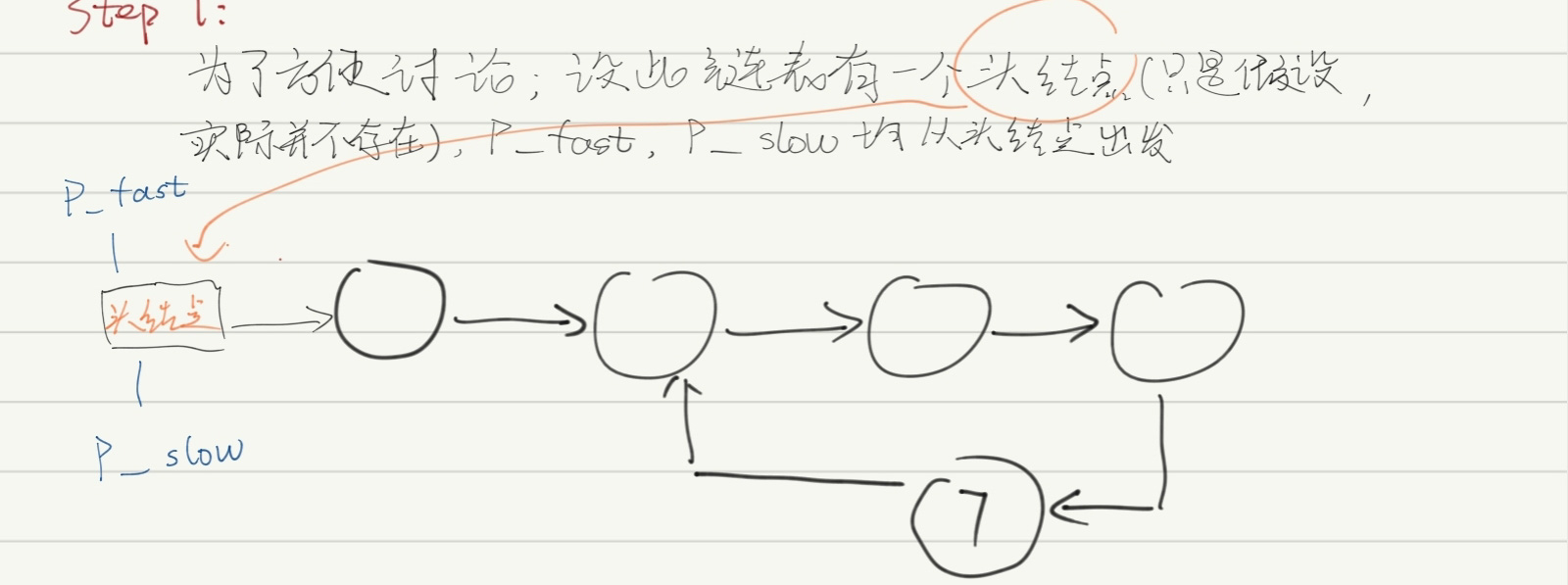
Step2：

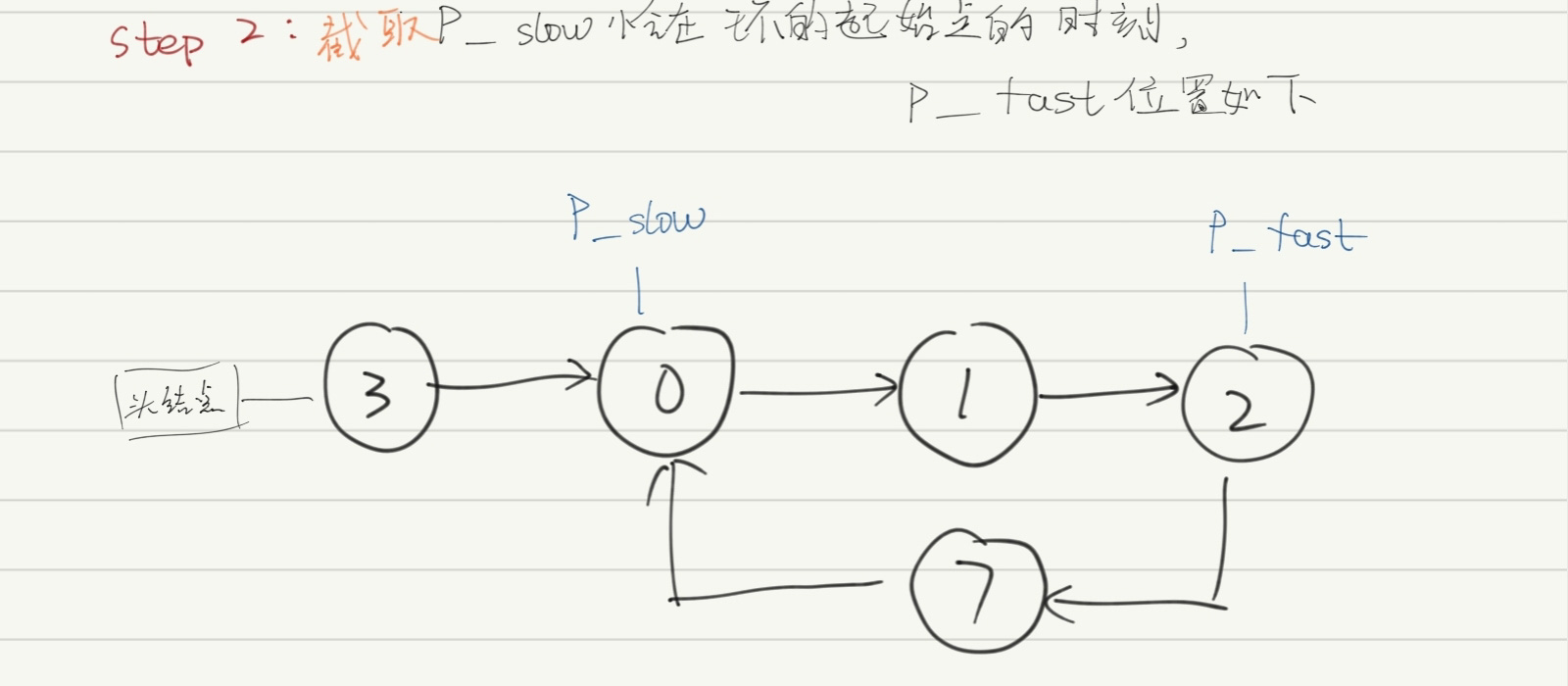
这是一个特殊的时间点，此时，
P_slow恰好走了num₁步，共走了T₁=num₁次;
P_fast走了2·num₁步，P_fast路程-P_slow路程=num₁步。

Step3：
此后，P_fast欲追上P_slow,需要再走num_环-num₁步，下图给出了形象的说明：

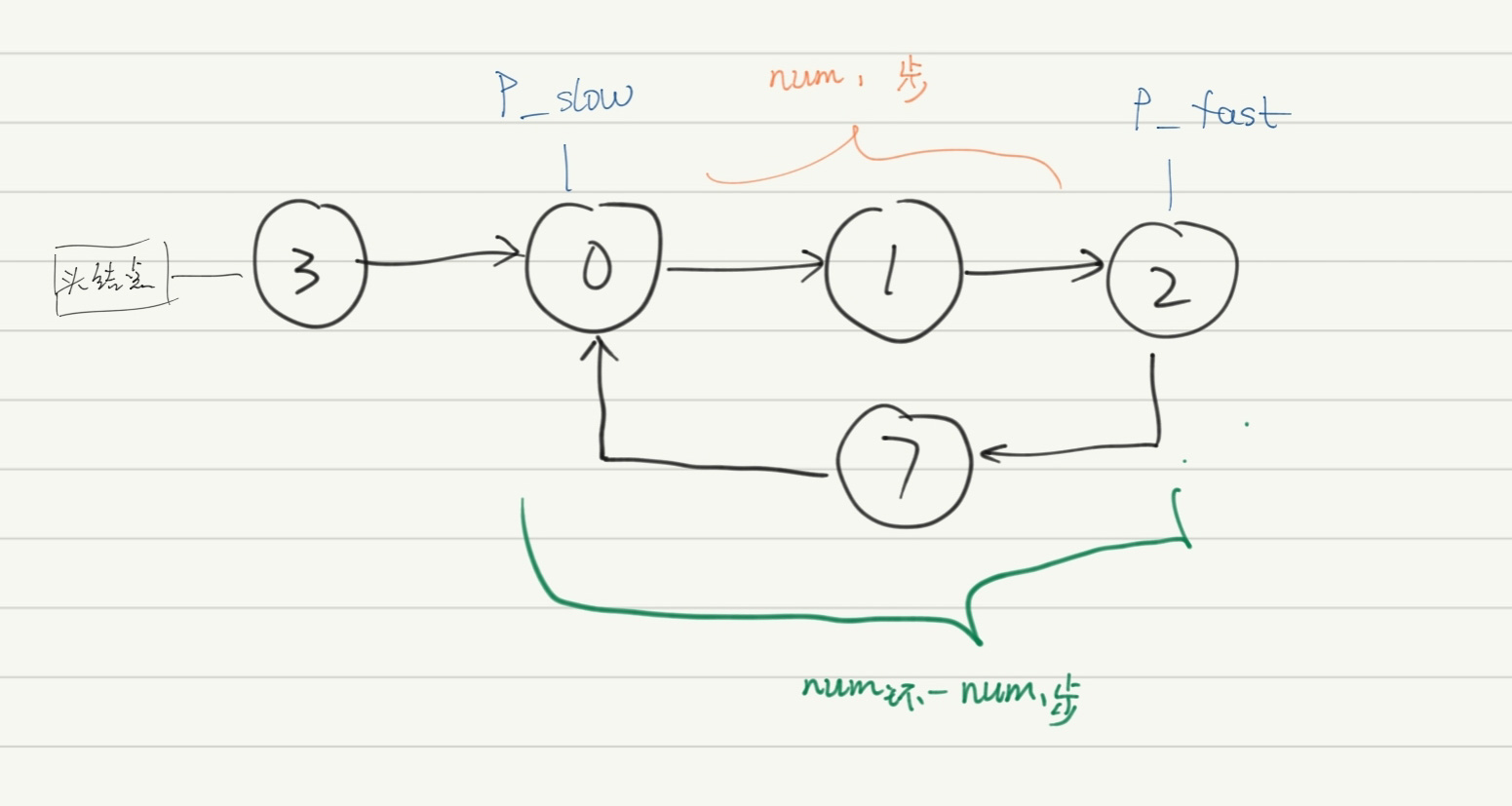
这时我们认为P_fast与P_slow速度差为1步/次，路程差=num_环-num₁步，
显然需要再走路程差/速度差次，
即再走 T₂=num_环-num₁ 次，P_fast才能追上P_slow。
把整个过程连起来看，一共走了T₁+T₂=num_环次，P_slow总路程k即为num_环步。

回忆一下我们第一个结论：

1.我们假设快慢指针都走了k次，最后有：P_fast总路程=2k，P_slow总路程=k；
则相遇时一定有：k为num_环整数倍，我简记作k=a·num_环（a为任意正整数);
已知k=a·num_环，能否尝试分析出此处a的值？
在Step3中我们分析出k=num_环，故a显然为1！

至此得出第二个结论：我们假设快慢指针都走了k次,
最后有：P_fast总路程=2k,P_slow总路程=k;
k为num_环整数倍，简记作k=a·num_环,a=1；

利用结论解题

这题的数学条件到目前就够用了，下面我们设置快慢指针，并设置一个变量i记录P_slow的路程，向前走一步就i++，若快慢指针若在环中相遇，则一定有：P_slow总路程=num_环；
借此我们可以由第一次相遇的位置得到num_环=P_slow总路程=i；

已知 num_环 的值，欲求环何时开始，我们再设计一组速度相同的前后指针P_front,P_back，P_front永远比P_back快 num_环 步，让P_front,P_back同时遍历，当P_front在P节点第一次追上P_back时，P节点即为环的起始点，如下图；到此为止，本题结束。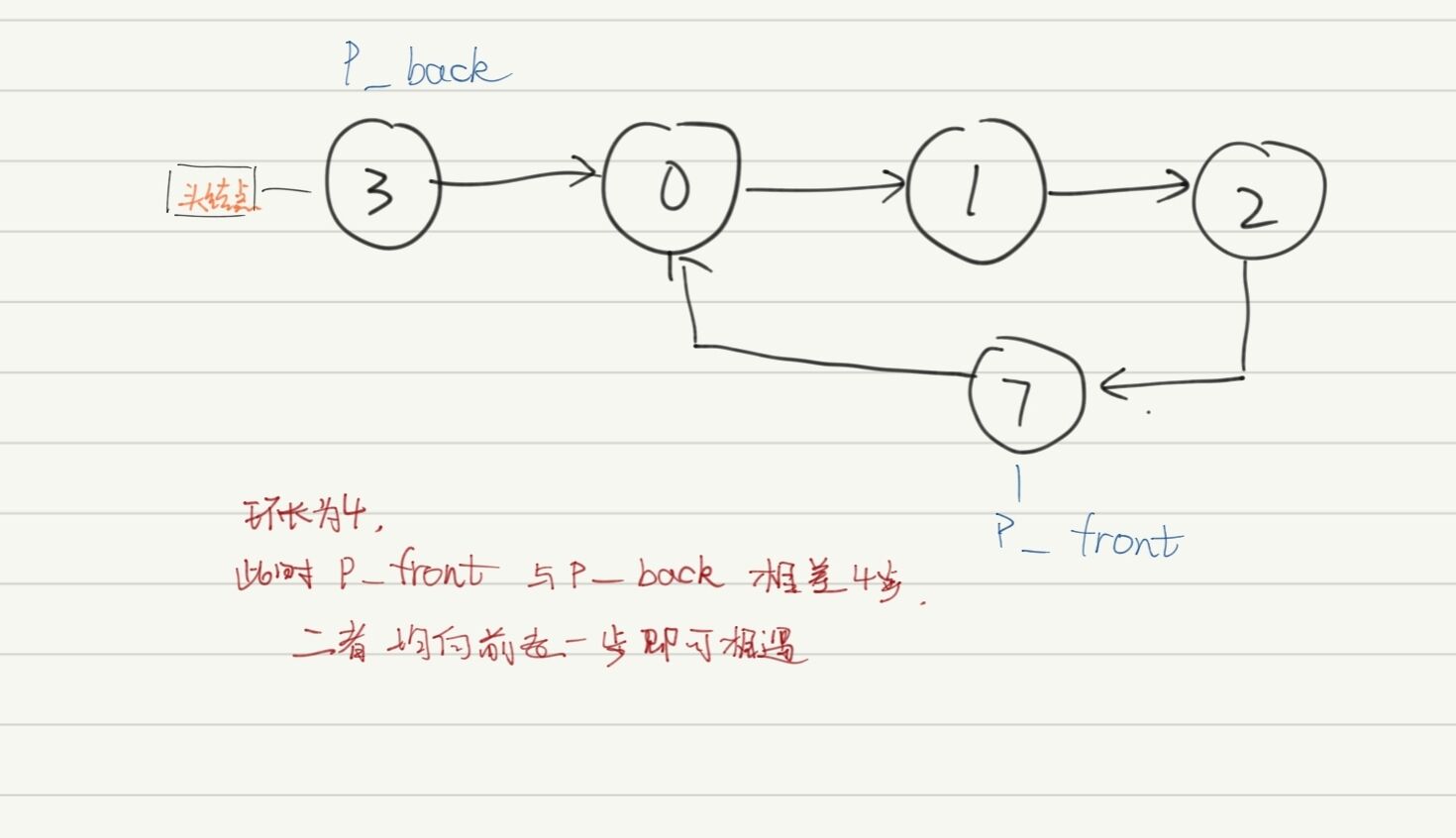

代码：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode slow = head, fast = head;
        while (fast != null) {
            slow = slow.next;
            if (fast.next != null) {
                fast = fast.next.next;
            } else {
                return null;
            }
            if (fast == slow) {
                ListNode ptr = head;
                while (ptr != slow) {
                    ptr = ptr.next;
                    slow = slow.next;
                }
                return ptr;
            }
        }
        return null;
    }
}

已知2k mod a=k mod a，则k mod a = 0，证明：
（摆烂了今天，这段明天再写
ps：以后应该不会这样更新了，以后只贴代码、题目、简单思路，这样更新下去我要吐血了

对于LC141:

对于LC142:

经分析可得两个结论

第一个结论

第二个结论

利用结论解题

代码：